Частина 1. Основи мереж електронних комунікацій

 

Дисципліна “ОТКРТ1 Основи мереж електронних комунікацій” є однією з базових дисциплін, яка розширює кругозір будь-якого радіоінженера. Цей предмет формує теоретичні знання та практичні навички з побудови, керування, модернізації, моніторингу та аналізу продуктивності, діагностики та розв’язання проблем сучасних електронних мереж і комунікацій.

Силабус курсу

Частина 2. Сигнали та процеси в радіотехніці

В курсі ” Основи теорії телекомунікацій і радіотехніки” розглядаються теорія сигналів і різноманітні радіотехнічні кола.

Після проходження курсу студент отримає знання про:

1. Теорія детермінованих керувальних та радіо сигналів.
2. Спектральний, операторний та кореляційний аналіз сигналів.
3. Лінійні перетворення аналогових сигналів.
4. Аналіз та розрахунок генераторів гармонічних коливань.
5. Теорія дискретизації сигналів.
6. Нелінійні та параметричні кола та процеси в них.
7. Пристрої, побудовані за допомогою нелінійних перетворювачів сигналів.

Силабус курсу

Основи програмування та алгоритми

Дисципліна включає в себе вивчення мови програмування С. Вибір даної мови програмування продиктовано широким її застосуванням при розробці програм для мікроконтролерів та мікропроцесорів, які вивчаються в подальших дисциплінах і є основою для розробки вбудованих систем, які все частіше застосовуються в різноманітних сферах. Крім того, вивчення мови програмування С шляхом виконання відповідних навчальних завдань є основою для опановування об’єктно-орієнтованої мови програмування С++, яка широко використовується на практиці, в тому числі і для реалізації складних інженерних рішень. Дисципліна «Інформатика1. Основи програмування та алгоритми» передбачає опанування мови програмування С через виконання відповідних завдань лабораторних робіт, які дозволяють сформувати відповідні навики, що будуть необхідні при подальшій практичній чи науковій діяльності. Сформовані навики, уміння та знання, що отримані в ході вивчення дисципліни  «Інформатика1. Основи програмування та алгоритми», дозволять створити базу для подальшого вивчення інших мов програмування, що широко використовуються в різних сферах галузі інформаційних технологій (ІТ) та стане потужною основою для професійного зростання та розширення сфери практичного застосування отриманих здобутків навчання.

Силабус курсу

Основи обчислювальної техніки

Предметом дисципліни є вивчення основ проектування цифрових пристроїв та функціональних вузлів, які використовуються в побутових та професійних апаратах.

Зараз практична більшість радіотехнічних пристроїв містять пристрої цифрової обробки інформації. Тому без ґрунтовних знань в області цифрової схемотехніки неможливо навчити майбутніх радіоінженерів розробляти сучасну електронну техніку, яка використовується майже в усіх областях діяльності людини.

Мета вивчення дисципліни – придбання знань, навиків і вмінь проектування цифрових пристроїв та їх використання в різноманітних радіотехнічних пристроях: побутових, обчислювальних та керувальних приладах і системах.

Завдання вивчення дисципліни: студент повинен вміти скласти та обґрунтувати технічне завдання на цифровий пристрій; розробити його структурну та електричну схеми; виконати необхідні електричні розрахунки; обґрунтувати та зробити вибір елементної бази.

Силабус курсу

Метою кредитного модуля є формування у студентів здатностей:

• Аналізувати дискретні системи та їх структури;
• Проектувати лінійні цифрові фільтри;
• Визначати основні характеристики дискретних сигналів;
• Використовувати основні методи спектрального аналізу дискретних сигналів;
• Проектувати дискретні системи з обробленням сигналів на кількох швидкостях.

Силабус курсу

Дисципліна “Процеси в лінійних електронних схемах” містить теоретичний матеріал із прикладами розв’язку практичних задач, що використовується на лекційних заняттях. В ході вивчення цієї дисципліни студетни мають отримати теоретичні та практичні навики при засвоєнні курсу. Дисципліна розгляає такі теми: апарат схемних функцій, перехідні процеси у колах першого та другого порядку, елементи спектрального аналізу, процеси у зв’язаних контурах та основи синтезу електроних схем. Запропнований курс є логічним продовженням курсу “Основи теорії кіл”

Силабус курсу

Основною ціллю курсу є ознайомлення студентів з особливостями проектування радіоелектронної апаратури. Навчити працювати з технічною документацією, орієнтуватися в елементній базі та вміти працювати з програмно-апаратною платформою Arduino.

Умовно курс можна поділити на дві чатини. В першій частину студенти пройдуть шлях від схеми електричної принципової до готового працюючого пристрою. Ознайомляться з програмою DipTrace, спроектують та виготовлять друковану плату, проведуть можтаж компонентів на неї, при потребі проведуть налаштування. Друга частина присвячена вивченню програмно-апаратної платформи Arduino. Студенти навчаться просто та швидко створювати цікаві та корисні електронні системи з мікроконтролерним керуванням.

Силабус курсу

Дисципліна «Вища математика» є однією з фундаментальних загальноосвітніх дисциплін, що складають теоретичну основу підготовки інженерів та програмістів. Знання та вміння, отримані студентом під час вивчення даної навчальної дисципліни, використовуються в подальшому при вивченні багатьох наступних дисциплін професійної підготовки фахівця з базовою та повною вищою освітою.  При проходженні даної дисципліни студенти ознайомляться: з функціями однієї змінної (область визначення, область значень, види та способи завдання функцій, основні характеристики функцій, основні елементарні функції та їх графіки); основами диференціального числення функцій однієї змінної (границя числової послідовності, границя функції, перша і друга визначні границі, еквівалентні нескінченно малі функції, неперервність функції,  точки розриву, дотична і нормаль до кривої, похідна та диференціал функції, асимптоти графіка функції, екстремум функції, правило Лопіталя, побудова графіків  функцій); основами інтегрального числення функцій однієї змінної (первісна, невизначні інтеграли).

Силабус курсу Вища математика 1

Силабус курсу Вища математика 2

Силабус курсу Вища математика 3

Дисцилпіна “Основи теорії кіл” містить теоретичний матеріал та приклади розв’язання задач щодо кіл постійного струму, змінного струму, коливальних контурів, прохідних чотириполюсників та схемних функцій, довгих ліній, операторний метод. При вивченні данного курсу  студенти мають одержати практичні навички при розв’язанні задач різного роду складності щодо розрахунку кіл постійного струму, змінного струму, коливальних контурів, схемних функцій та чотириполюсників, розрахунку кіл класичним, операторним та часовим методами. Дисципліна буде корисна студентам, що мають на меті засвоїти теоретичний та практичний курс з дисципліни «Основи теорії кіл»

Силабус курсу

Електронна компонентна база

Метою навчальної дисципліни є формування у студентів компетентностей:

• набуття знань про сучасну компонентну базу РЕА; будову і принцип дії, характеристики та параметри електронних приладів та інтегральних мікросхем (ІС), основні напрямки їх розвитку;
• набуття знань про вплив конструкцій та властивостей матеріалів на  характеристики компонентів, а також про вплив технологічного розкиду та умов експлуатації на основні параметри компонентів РЕА, електронних приладів та ІС;
• навчитися застосовувати набуті знання для правильного вибору схемотехнічних рішень при розробці РЕА;
• набуття навичок вимірювання параметрів, електронних компонентів, об’єктивної оцінки функціональних та параметричних можливостей компонентної бази РЕА.

Силабус курсу

Аналогова схемотехніка

Метою навчальної дисципліни є формування у студентів здатностей:

•  Аналізувати схемотехнічні рішення окремих каскадів підсилення та підсилювальних пристроїв різного призначення;
•  Розробляти технічні завдання на проектування електронних пристроїв;
•  Розробляти структурні та принципові схеми підсилювальних пристроїв різного призначення;
•  Проектувати каскади підсилення та підсилювальні пристрої різного призначення;
•  Визначати та вимірювати основні параметри та характеристики підсилювальних пристроїв.

Силабус курсу

Навчальна дисципліна «Електродинаміка та поширення радіохвиль» присвячена вивченню основних властивостей електромагнітного поля, набуття студентами конкретних знань про поширення електромагнітних хвиль. Студенти навчаються визначати основні характеристики електромагнітних хвиль; формувати електромагнітні хвилі з різними видами поляризації; вимірювати поляризаційні діаграми і визначати за ними поляризацію хвиль; розв’язувати крайові задачі електродинаміки; розраховувати і вимірювати параметри ліній передачі і резонаторів; вимірювати розподіли полів у лініях передачі та резонаторах.

Силабус курсу

Основною метою викладення цієї дисципліни полягає у наданні студентам усвідомлення відповідальності за особисту та колективну безпеку та здатностей для її оцінки і забезпечення на робочих місцях і у підрозділах під час майбутньої професійної діяльності на первинній посаді, а також формування та набуття студентами компетентностей, знань, умінь та навичок, необхідних для здійснення їх професійної діяльності з урахуванням ризику виникнення небезпечних та надзвичайних ситуацій (аварій, пожеж тощо), які можуть привести до несприятливих наслідків на об’єктах господарської діяльності під час виконування обов’язків технічних фахівців в галузі електроніки та телекомунікацій або операторів радіо- та телекомунікаційного устаткування.

Силабус курсу

Курс «Економіка і організація виробництва» є базовою загальноекономічною дисципліною для майбутніх фахівців – інженерів, оскільки охоплює усі ключові розділи прикладної економіки, організації та забезпечення ефективного господарювання на рівні підприємства.

Предмет дисципліни включає вивчення теорії і практики господарювання на рівні підприємства в ринкових умовах; конкретних форм та методів господарювання; принципів формування та використання виробничого потенціалу; взаємодію всіх видів ресурсів; організацію і ефективність господарської діяльності підприємства.

Метою кредитного модуля є формування у студентів економічної складової професійної підготовки майбутніх фахівців, яка інтегрує їх здатності: здатність працювати в команді.

Силабус курсу

Навчальна дисципліна складається з двох частин:

• Частина 1. «Інтелектуальна власність та патентознавство – 1. Право інтелектуальної власності» (забезпечує кафедра Інтелектуальної власності та приватного права Факультету соціології і права).
• Частина 2. «Інтелектуальна власність та патентознавство – 2. Патентознавство та набуття прав» (забезпечує кафедра Конструювання машин Механіко-машинобудівного інституту).

Метою навчальної дисципліни є підготовка фахівця, який має базові компетенції з права інтелектуальної власності, зокрема щодо законодавства та системи правової охорони інтелектуальної власності в Україні, їх критеріїв правової охорони та строків чинності майнових прав, оцінки, комерціалізації, та договірних способів розпоряджання майновими правами інтелектуальної власності та захисту прав інтелектуальної власності, створення об’єктів інтелектуальної власності, здійснення патентних досліджень за базами даних Укрпатенту, регіональних відомств та Всесвітньої організації інтелектуальної власності, набуття прав (державна реєстрація прав) на об’єкти права інтелектуальної власності.

Силабус курсу

Метою навчальної дисципліни “Пристрої надвисоких частот” є формування у студентів здатностей: розраховувати основні параметри різних типів пристроїв НВЧ, обирати найбільш ефективні пристрої НВЧ для радіотехнічних систем для заданих режимів роботи пристроїв і необхідних характеристик антенно-фідерного тракту, формулювати вимоги до елементів антенно-фідерного тракту, виходячи з їхнього функціонального призначення.

Навчальна дисципліна «Пристрої надвисоких частот» розглядає елементи антенно-фідерного тракту (без антен), їх характеристики і параметри та процеси, що супроводжують їх роботу. На лекціях розглядаються такі основні теми: основні характеристики ліній передачі (коаксіальних, хвилевідних, мікросмужкових, щілинних); математична модель регулярної лінії передачі; функціональне призначення, принципи роботи, характеристики основних елементів антенно-фідерного тракту (узгоджені і реактивні навантаження, ізолятори, роз’єми, обертальні з’єднання, переходи, перетворювачі типів хвиль, повороти ліній передачі); характеристика багатополюсників за допомогою матриць опорів, розсіювання і передачі, основні підходи до розрахунку елементів матриць розсіювання простих пристроїв НВЧ (трійників, подільників потужності, циркуля торів, вентилів); принципи дії і характеристики хвилевідних і мікросмужкових направлених відгалужувачів і подільників потужності; синтез простих фільтрів НВЧ; принцип побудови і характеристики керованих пристроїв НВЧ на основі феритів і із використанням p-i-n діодів. Практичні заняття і розрахунково-графічні завдання присвячені виконанню розрахунків вузькосмугових та широкосмугових узгоджуючи пристроїв коаксіального, мікросмужкового і хвилевідного виконання. На лабораторних роботах проводяться експериментальні дослідження характеристик і параметрів пристроїв НВЧ (подільників потужності, напрямлених відгалужувачів, прохідних резонаторів, феритових пристроїв)

Силабус курсу

В курсі “Статистична радіотехніка” розглядається новий підхід, за допомогою якого зовсім по новому вирішується задача обробки сигналів, та їх проходження через різні пристрої та системи.

Після проходження курсу студент отримає знання про:

1. Основи теорії статистики по відношенню до радіотехніки.
2. Використання статистики для опису та обробки результатів експериментів.
3. Кореляційна обробка сигналів.
4. Що таке випадкові сигнали, і як створювати для них математичний опис.
5. Які бувають шуми, і як їх враховувати при проходженні сигналів.
6. Проходження випадкових сигналів через лінійні та нелінійні кола.
8. Що таке оптимальна фільтрація та для чого потрібен оптимальний фільтр.

Новий підхід до обрахунку сигналів, що отримано в цьому курсі, дозволить слухачам обробляти результати будь-яких експериментів. Створювати системи виявлення сигналів, засновані на кореляційній обробці, з урахуванням існуючих шумів та завад. Наприклад системи зв’язку в Wi-Fi діапазоні з урахуванням завад від базових станцій мобільних операторів, або визначення сигналу відбитого від дрону, про тому, що існує спеціально створена завада, та ін. Також студент зможе розраховувати проходження сигналів з урахуванням шумів.

Силабус курсу

Метою вивчення дисципліни ОМ є ознайомлення з основними поняттями вимірювань, похибками, видами сигналів та основними методами оброблення вимірювальної інформації щодо параметрів радіотехнічних пристроїв.

За навчальним планом дисципліна ОР складається з лекційних  та лабораторних занять. В залежності від обсягу аудиторного часу, наданого за робочим навчальним планом, окремі теоретичні розділи дисципліни можуть бути винесені на самостійне опрацювання.   Вивчення дисципліни ОМ відбувається протягом одного семестру у вигляді одного кредитного модулю.

Силабус дисципліни

Знання та вміння, набуті в результаті вивчення дисципліни, забезпечують можливість працювати в організаціях та компаніях, що займаються організацією, проектуванням та експлуатацією наземного мобільного зв’язку.

Після проходження даного курсу слухач буде знати: принципи побудови та функціонування сучасних та перспективних систем мобільного зв’язку.

Знання та вміння, набуті в результаті вивчення дисципліни, забезпечують можливість працювати в організаціях та компаніях, що займаються організацією, проектуванням та експлуатацією наземного мобільного зв’язку.

Силабус курсу

Навчальна дисципліна Електромагнітна сумісність РЕС присвячена вивченню взаємного впливу та радіоелектронних систем та їх завадозахищеності. Студенти навчаться оцінювати та вимірювати на практиці сумісність таких систем як бездротові мережі, НВЧ прилади, мобільні системи зв’язку та ін

Силабус курсу

Метою викладення дисципліни «Дискретні і цифрові сигнали та процеси в радіотехніці» є:

• Набуття знань з теорії дискретних сигналів, а також практичних навичок і вмінь використання методів їх перетворення при аналізі і синтезі систем дискретного часу, усвідомлення фундаментальності такої теорії і можливості її застосування до більш широкого класу сигналів і систем, які не є цифровими і не охоплюються теорією ЦОС.
• Створення теоретичного фундаменту для подальшого вивчення методів, алгоритмів і особливостей практичної реалізації процесів формування сигналів дискретного часу та їх обробки на базі пристроїв з обмеженою розрядністю і швидкодією в рамках дисциплін ЦОС, ЦП, СПвРС.

Силабус курсу

Супутникові інформаційні системи (СІС) – це інформаційні системи, в яких передача інформації здійснюється по радіоканалах з використання штучних супутників Землі, як ретрансляторів (у випадку телекомунікаційних систем) або джерел інформації (у випадку навігаційних супутників або супутників дистанційного зондування Землі). Це повністю автономна система, здатна обробляти і/або передавати інформацію. СІС мають незаперечні переваги над наземними телекомунікаційними системами завдяки спроможності охоплювати великі території Землі незалежно від характеру ландшафту, забезпечувати мобільність і  можливість швидкого розгортання у зонах стихійного лиха, гарячих точках тощо. Сучасні СІС спроможні забезпечувати інформаційну глобалізацію, лозунгом якої є “Communication with anybody,  anywhere, at any time” (Зв’язок з будь-ким у будь-якому місці в будь-який час).

Силабус курсу

Метою вивчення дисципліни “Основи наукових досліджень” є формування у студентів знання принципів  підготовки та методології організації і проведення  наукових досліджень, оформлення і захисту їх результатів. Зокрема надати студентам таких знань, які дадуть їм можливість вирішувати комплексні задачі з виконання  наукових досліджень, спрямованих на розробку нових та вдосконалення існуючих радіоелектронних та радіотехнічних приладів, систем і комплексів, та захист на цій основі підготовлених ними магістерської дисертації.

Силабус курсу

Метою вивчення дисципліни “Основи наукових досліджень” є формування у студентів знання принципів  підготовки та методології організації і проведення  наукових досліджень, оформлення і захисту їх результатів. Зокрема надати студентам таких знань, які дадуть їм можливість вирішувати комплексні задачі з виконання  наукових досліджень, спрямованих на розробку нових та вдосконалення існуючих радіоелектронних та радіотехнічних приладів, систем і комплексів, та захист на цій основі підготовлених ними магістерської дисертації.

Силабус курсу

На сьогодні медичні кількість різновидів медичних засобів діагностики і лікування становить більше 40 000 одиниць. На (95-97) % вони є або повністю радіоелектронними, або частково у своєму складі мають елементи радіоелектроніки.

В сучасних умовах медичному радіоелектронному приладобудуванню приділяється значна увага. Це обумовлюється необхідністю рішення глобальної задачі – оснастити заклади охорони здоров’я сучасним медичним обладнанням, приладами і інструментами, насамперед такими: а) рентгенівськими комплексами; б) комп’ютерними томографами; в) ультразвуковою, електронною, ендоскопічною технікою; г) лабораторними аналізаторами; д) системами неперервного спостереження за хворими, дітьми і особами похилого віку; е) обчислювальною технікою; ж) засобами малої механізації.

Сучасні засоби біомедичної діагностики і лікування представляють собою складні технічні системи, які втілюють у собі останні новітні знання і технології, що отримані у різних галузях науки і техніки, зокрема у радіоелектроніці і радіофізиці. Радіофізика і радіоелектроніка, як наукові методології одержання інформації про дистантні об’єкти, досягли видатних успіхів у вивченні Космосу, Землі, Океану. Ця інформація є інтегральною, вона відображає основні системні закономірності структури функціонування зазначених об’єктів. В останні десятиліття організм людини також розглядається як радіофізичний об’єкт, зокрема і як дистантний, створюються відповідні радіоелектронні засоби діагностики і лікування. В результаті взаємодії біологів, радіофізиків, біофізиків, фізіологів, математиків, лікарів і інженерів розвиваються такі основні напрямки застосування радіоелектронних методів у біології і медицині.

Силабус курсу

Навчальна дисципліна «Математичні методи оптимізації» є важливою компонентою в формуванні теоретичної бази для подальшого вдосконалення, поглиблення та розвинення знань та умінь випускника університету у напрямку проектування оптимальних конструкцій для різних галузей промисловості, а також вивчення та професійного використання комп’ютерних САD систем. Набуті знання та вміння застосовуються при розробці та аналізі математичних моделей конструкцій та використанні сучасного програмного забезпечення для проектування і розрахунків елементів радіотехнічних пристроїв та систем.

При вивченні дисципліни студенти формують здатність обирати найбільш ефективні методи оптимізації для пошуку оптимальних рішень, формулювати постановки задач оптимального проектування радіотехнічних пристроїв та систем, розв’язувати практичні задачі пошуку екстремуму цільових функцій і оптимізації систем і процесів, реалізовувати методи оптимізації та математичні моделі дослідження операцій у середовищі MATLAB  та інтерпретувати та застосовувати результати розв’язання задач в практичних цілях при прийнятті рішень.

Основні теми, що розглядаються в рамках курсу:

– ­основні методи лінійного програмування.

– основні методи одновимірної оптимізації;

– основні методи прямого пошуку (метод покоординатного спуску, метод пошуку по зразку, симплексний метод Нелдера-Міда);

– основні методи першого порядку (алгоритм найшвидшого спуску, метод спряжених градієнтів) та другого порядку (методу Ньютона і квазіньютоновські методи – метод Бройдена, метод Девідсона-Флетчера-Пауелла, алгоритм Пірсона;

– природні алгоритми глобальної оптимізації (генетичний алгоритм, алгоритму бджолиного рою, метод відпалювання);

– методи умовної (штрафні та бар’єрні функції, метод множників Лагранжа) та багатокритеріальної оптимізації (поняття фронту Парето, алгоритми VEGA, NSGA, NSGA-II);

– методи просторового відображення в задачах оптимізації радіотехнічних пристроїв та систем – Алгоритми Space Mapping та Aggressive Space Mapping.

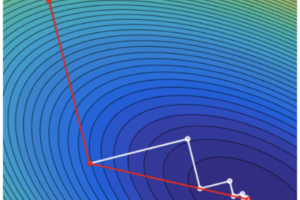
На практичних заняттях розглядається реалізація алгоритмів оптимізації у середовищі MATLAB і досліджуються складні функції для отримання досвіду обирати методи оптимізації, враховуючи особливості цільової функції

Силабус курсу

Навчальна дисципліна “СМАРТ-системи” дає знання архітектури цифрових антенних решіток, системних характеристик складових компонентів цифрових антенних решіток: ЦАП, АЦП, підсилювачів потужності, комутуючих пристроїв, малошумлячих підсилювачів, антенних решіток, принципів побудови антенних решіток MIMO-систем, методів визначення напрямку приходу сигналу та методів цифрового формування діаграми спрямованості. Після вивчення курсу студенти матимуть здатність обирати найбільш ефективні елементи для приймально-передавальних пристроїв цифрових антенних решіток, які працюють в різних частотних діапазонах, проводити інженерні розрахунки основних характеристик елементів приймально-передавальних пристроїв цифрових антенних решіток, виконувати розрахунок системних характеристик приймально-передавальних пристроїв цифрових антенних решіток та моделювати роботу методів визначення напрямку приходу сигналу у програмі MATLAB.

Дисципліна складається з двох розділів:

– Приймально-передавальні модулі СМАРТ-систем

– Цифрове формування діаграми спрямованості в СМАРТ-системах

Перший розділ супроводжується комп’ютерним практикумом у AWR DESIGN ENVIRONMENT, другий розділ – у MATLAB.

Силабус курсу

Дисципліна “Антенні системи” охоплює сучасний рівень розвитку антен для нового покоління радіелектронних систем різноманітного призначення. Дисципліна “Антенні системи” зокрема охоплює дводзеркальні антени (Касегрена, Грегорі, АДЕ, АДГ, багатопроменеві, косчмічні тощо), класичні фазовані антенні решітки, активні фазовані антенні решітки, цифрові антенні решітки тощо.

Студенти після засвоєння кредитного модуля мають продемонструвати такі результати навчання:

знання:

– принципів побудови, конструкцій, принципів дії сучасних антенних систем, їх елементів та фізичних процесів, що в них відбуваються; увагу студентів сфокусовано насамперед на дводзеркальних антенних системах різного типу, планарних антенних решітках та скануючих антенних решітках різних типів, в тому числі багатоканальних.

• гранично-досяжних параметрів, застосування та обмеження антенних систем різних типів;
• методів розрахунків та вимірювання параметрів антенних систем;
• методики експериментального дослідження характеристик антенних систем.

уміння:

– провести попередні інженерні розрахунки основних параметрів антенних систем різних типів;

• вибрати найбільш ефективні типи антенних систем для радіотехнічних систем, які працюють в різних частотних діапазонах;
• правильно побудувати схему вимірювання характеристик антенних систем;
• провести експериментальне дослідження характеристик і параметрів антенних систем різних типів.

досвід:

– інженерна обробка інформації стосовно антенних систем різних типів;

• експериментального дослідження характеристик антенних систем;

– роботи з вимірювальною апаратурою НВЧ діапазону та дослідними зразками антенних систем різних типів

 

Силабус навчальної дисципліни